Hình chóp là một phần kiến thức hình học quan trọng trong chương trình toán lớp 8, học kì 2. Dưới đây là tổng kết về định nghĩa hình chóp, tính chất, công thức tính chu vi, diện tích, thể tích các loại hình chóp. Bên cạnh đó, chúng ta cũng sẽ tìm hiểu về các loại hình chóp ít được nhắc đến trong sách giáo khoa.

Định nghĩa hình chóp là gì?
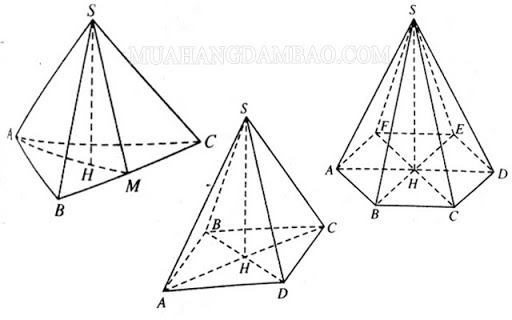
Hình chóp là một hình không gian có mặt đáy là một đa giác lồi và các mặt bên đều là các tam giác có cùng một đỉnh, gọi là đỉnh của hình chóp.
- Hình chóp có nhiều loại khác nhau, tên của chúng được đặt dựa trên đáy.
- Nếu đáy là một tam giác, ta gọi đó là hình chóp tam giác. Nếu đáy là một tứ giác, ta gọi đó là hình chóp tứ giác.
- Trong trường hợp đặc biệt, nếu đáy là một tam giác đều hoặc tứ giác đều, ta gọi đó là hình chóp đều.
Tính chất của hình chóp:
- Đường thẳng đi qua một đỉnh và vuông góc với mặt phẳng đáy được gọi là đường cao của hình chóp.
- Tên gọi của hình chóp dựa vào đa giác mặt đáy: hình chóp có đáy là tam giác được gọi là hình chóp tam giác, hình chóp có đáy là tứ giác gọi là hình chóp tứ giác.
- Nếu các cạnh bên hợp với mặt đáy tạo các góc bằng nhau hoặc các cạnh bên bằng nhau, chân đường cao là tâm đường tròn ngoại tiếp đáy.
- Nếu các mặt bên hợp với mặt đáy tạo các góc bằng nhau hoặc các đường cao từ các mặt bên xuất phát từ cùng một đỉnh bằng nhau, chân đường cao là tâm đường tròn nội tiếp mặt đáy.
- Nếu mặt bên hoặc mặt chéo vuông góc với mặt phẳng đáy, đường cao của hình chóp sẽ là đường cao của mặt bên hoặc mặt chéo đó.
Các loại hình chóp thường gặp
Hình chóp tam giác đều là gì?
Định nghĩa:
Hình chóp tam giác đều là hình chóp có đáy là một tam giác đều, các mặt bên là các tam giác cân bằng nhau có cùng đỉnh.
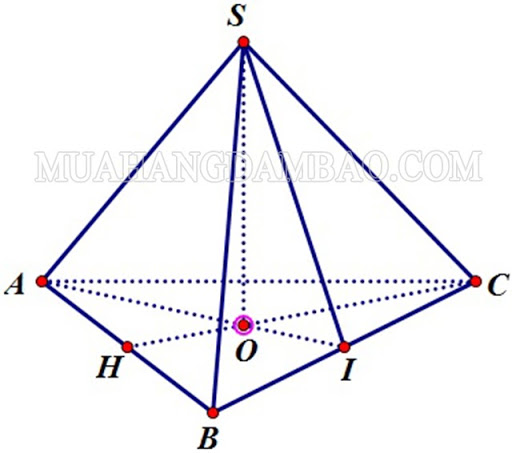
Tính chất:
- Hình chóp tam giác đều có 3 mặt phẳng đối xứng.
- Hình chóp có đáy là tam giác đều.
- Các cạnh bên bằng nhau.
- Tất cả các mặt bên đều là các tam giác cân bằng nhau.
- Chân đường cao trùng với tâm của mặt đáy (tâm đáy là trọng tâm của tam giác).
- Tất cả các góc tạo bởi các mặt bên và mặt đáy đều bằng nhau.
- Tất cả các góc tạo bởi cạnh bên và mặt đáy đều bằng nhau.
Lưu ý: Tâm của tam giác đều là giao điểm của 3 đường trung tuyến và cũng là đường cao, trung trực và phân giác trong.
Hình chóp tứ giác đều là gì?
Định nghĩa:
Hình chóp tứ giác đều là hình chóp có đáy là một hình vuông, các mặt bên là các tam giác cân bằng nhau có cùng đỉnh.
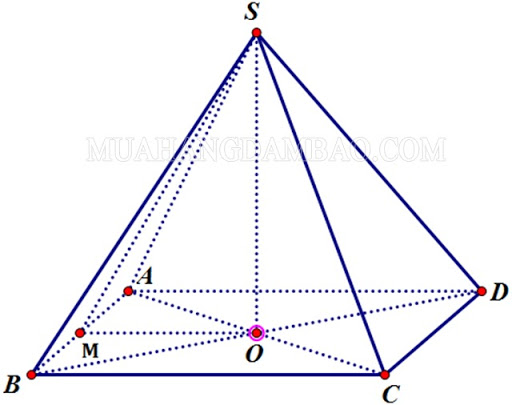
Tính chất:
- Hình chóp có đáy là hình vuông.
- Các cạnh bên bằng nhau.
- Tất cả các mặt bên đều là các tam giác cân bằng nhau.
- Chân đường cao trùng với tâm của mặt đáy (tâm đáy là giao điểm của 2 đường chéo).
- Tất cả các góc tạo bởi cạnh bên và mặt đáy bằng nhau.
- Hình chóp tứ giác có 8 cạnh.
Hình chóp cụt đều là gì?
Định nghĩa:
Hình chóp cụt đều là hình chóp đều bị cắt bởi một mặt phẳng song song với đáy. Phần hình chóp nằm giữa mặt phẳng đó và mặt phẳng đáy của hình chóp gọi là hình chóp cụt đều.
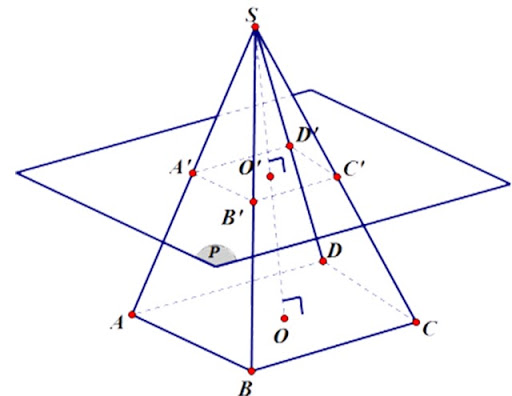
Tính chất:
- Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
Công thức tính chu vi, diện tích, thể tích hình chóp
Công thức tính chu vi hình chóp (Áp dụng cho hình chóp tam giác, hình chóp tứ giác)
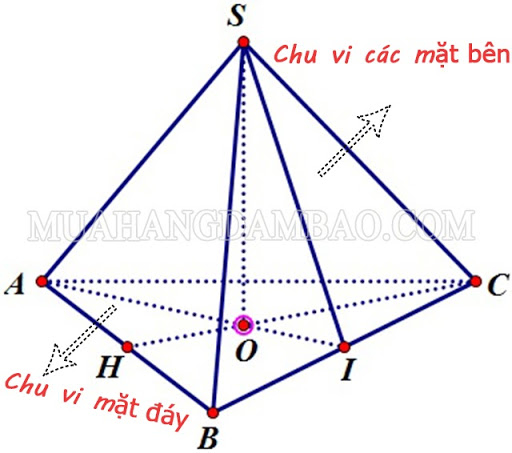
Chu vi hình chóp bằng tổng chu vi mặt đáy và các mặt bên.
Công thức:
P = Pđáy + Pcác mặt bên
Trong đó:
Pđáy là chu vi mặt đáy
Pcác mặt bên là chu vi các mặt bên
Công thức tính diện tích hình chóp đều (Áp dụng cho hình chóp tam giác, hình chóp tứ giác)
Diện tích hình chóp gồm diện tích xung quanh và diện tích toàn phần.
Diện tích xung quanh
Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn.
Công thức
Sxq = p.d

Trong đó:
- p là nửa chu vi đáy
- d là trung đoạn của hình chóp. Trung đoạn là đường cao xuất phát từ đỉnh xuống trung điểm của một cạnh.
Diện tích toàn phần của hình chóp:
Diện tích toàn phần của hình chóp bằng tổng diện tích xung quanh và diện tích đáy.
Stp = Sxq + Sđáy
Để tính được diện tích xung quanh và toàn phần của hình chóp, chúng ta cần tính độ dài trung đoạn và chu vi, diện tích đáy.
Thể tích hình chóp (Áp dụng cho hình chóp tam giác, hình chóp tứ giác)
Công thức
V = 1/3S.h
Trong đó:
- S là diện tích đáy,
- h là chiều cao.
Thể tích hình chóp cụt 4 cạnh
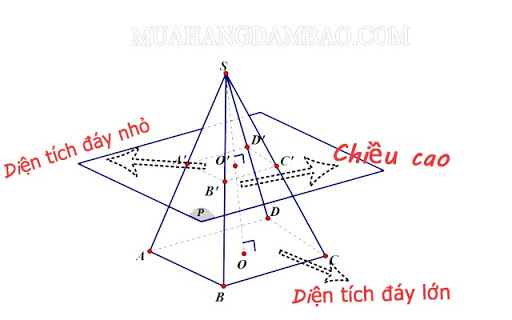
Công thức:
Trong đó:
- B’ và B lần lượt là diện tích của đáy nhỏ và đáy lớn của hình chóp cụt đều.
- h là chiều cao (khoảng cách giữa hai mặt đáy).
Phân biệt các hình chóp
| Đáy | Mặt bên | Số cạnh đáy | Số cạnh | Số mặt |
|---|---|---|---|---|
| Tam giác đều | Tam giác cân | 3 | 6 | 4 |
| Vuông | Tam giác cân | 4 | 8 | 5 |
| Ngũ giác đều | Tam giác cân | 5 | 10 | 6 |
| Lục giác đều | Tam giác cân | 6 | 12 | 7 |
Dạng bài tập về hình chóp
Để xác định mối quan hệ giữa các yếu tố cạnh và mặt phẳng trong hình chóp đều và hình chóp cụt đều, chúng ta có thể sử dụng mối quan hệ song song và vuông góc giữa các đường thẳng và mặt phẳng và áp dụng kiến thức về hình chóp đều.
Ví dụ bài tập:
Bài 1: Cho hình chóp SABC có SA vuông góc với mặt phẳng (ABC) và đáy ABC là tam giác vuông tại B, AB = a, SA = a. Lấy điểm H là hình chiếu của A trên cạnh SB. Khoảng cách giữa AH và BC bằng bao nhiêu?

Đáp án:
Ta có BC ⊥ AB VÀ BC ⊥ SA → BC ⊥ (SAB) → BC ⊥ HB
Mà AH ⊥ HB → HB là đoạn vuông góc chung của AH và BC → d(AH, BC) = HB
Tam giác SAB vuông cân tại A có SA = SB = a, AH ⊥ SC
→
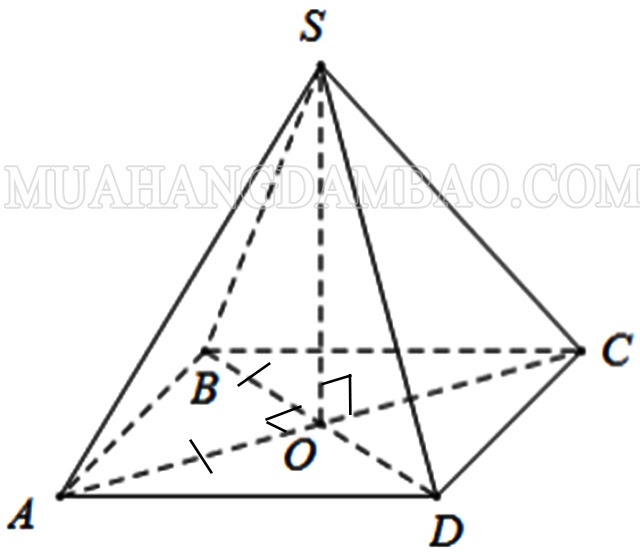
Bài 2: Cho hình chóp S ABCD là chóp tứ giác đều có các mặt bên là các tam giác đều, AB = 8m, O là trung điểm của AC. Hình chóp S ABCD có bao nhiêu cạnh? Độ dài SO là bao nhiêu?
Đáp án:
Hình chóp S ABCD là hình chóp tứ giác nên có 8 cạnh.
Hình chóp S ABCD đều nên đáy ABCD là hình vuông ΔOAB vuông cân tại O
Áp dụng định lí Py-ta-go vào tam giác vuông ΔOAB có
AB² = OB² + OB² → AB² = 2OA²
Hình chóp có các mặt bên là tam giác đều nên ΔSAB là tam giác đều. Do đó, SA = AB = 8m
Ta có SO ⊥ OA nên SOA vuông tại O
Áp dụng định lí Py-ta-go vào tam giác vuông SOA ta có:
SB² = OS² + OA²
Hy vọng thông qua bài tổng hợp kiến thức về hình chóp trên đây, bạn đã hiểu và ghi nhớ được các công thức tính chu vi, diện tích, thể tích hình chóp và phân biệt được các loại hình chóp với nhau. Chúc bạn có những giờ học thú vị và bổ ích.
Được chỉnh sửa bởi: HEFC
