Độ tuyến tính là một khái niệm quan trọng trong thống kê, đặc biệt là khi bạn muốn tìm hiểu mối quan hệ giữa hai biến. Trong bài viết này, chúng ta sẽ tìm hiểu về độ tuyến tính, từ khái niệm đến cách tính toán, ứng dụng và hạn chế của nó.
Khái niệm độ tuyến tính
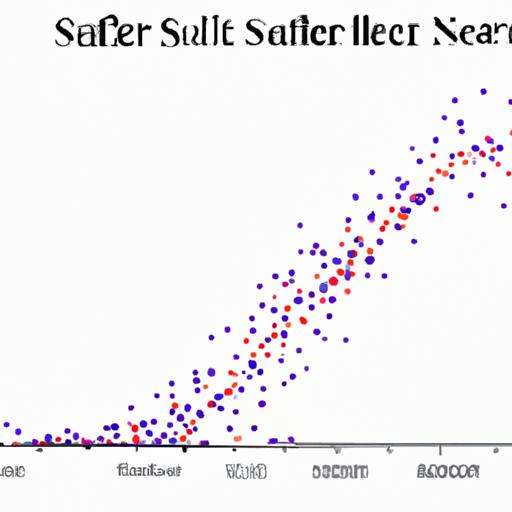
Độ tuyến tính là một đại lượng đo lường mức độ tương quan giữa hai biến. Nó thường được ký hiệu bằng r hoặc rxy và có giá trị nằm trong khoảng từ -1 đến 1. Khi giá trị của độ tuyến tính tiến gần đến -1 hoặc 1, thì mối quan hệ giữa hai biến càng mạnh. Nếu giá trị độ tuyến tính bằng 0, thì hai biến không có mối quan hệ tuyến tính nào cả.
Ứng dụng của độ tuyến tính trong thống kê
Độ tuyến tính được sử dụng rộng rãi trong thống kê để đánh giá mối quan hệ giữa hai biến. Nó giúp chúng ta đánh giá mức độ tương quan giữa hai biến và dự đoán giá trị của một biến dựa trên giá trị của biến khác. Độ tuyến tính cũng được sử dụng trong các phân tích hồi quy, giúp chúng ta xác định mức độ ảnh hưởng của một biến đến biến phụ thuộc.
Trong bài viết tiếp theo, chúng ta sẽ tìm hiểu cách tính toán độ tuyến tính.
Cách tính toán độ tuyến tính
Công thức tính độ tuyến tính
Để tính toán độ tuyến tính giữa hai biến, chúng ta sử dụng công thức sau đây:
r = (Σ(x – x̄)(y – ȳ)) / (sqrt(Σ(x – x̄)^2) * sqrt(Σ(y – ȳ)^2))
Trong đó:
- r là độ tuyến tính giữa hai biến
- x và y là các giá trị của hai biến
- x̄ và ȳ là giá trị trung bình của hai biến
- sqrt là hàm tính căn bậc hai
Ví dụ minh họa cách tính toán độ tuyến tính
Giả sử bạn muốn tính độ tuyến tính giữa số giờ học và điểm số của một nhóm sinh viên. Bạn thu thập được dữ liệu như sau:
| Số giờ học | Điểm số |
|---|---|
| 1 | 60 |
| 2 | 70 |
| 3 | 80 |
| 4 | 90 |
| 5 | 100 |
Để tính độ tuyến tính giữa hai biến này, ta sẽ làm như sau:
- Tính giá trị trung bình của số giờ học và điểm số.
x̄ = (1+2+3+4+5)/5 = 3
ȳ = (60+70+80+90+100)/5 = 80
- Tính các giá trị (x – x̄) và (y – ȳ).
| Số giờ học | Điểm số | (x – x̄) | (y – ȳ) |
|---|---|---|---|
| 1 | 60 | -2 | -20 |
| 2 | 70 | -1 | -10 |
| 3 | 80 | 0 | 0 |
| 4 | 90 | 1 | 10 |
| 5 | 100 | 2 | 20 |
- Tính Σ(x – x̄)(y – ȳ), Σ(x – x̄)^2 và Σ(y – ȳ)^2.
Σ(x – x̄)(y – ȳ) = (-2 -20) + (-1 -10) + (0 0) + (1 10) + (2 * 20) = 100
Σ(x – x̄)^2 = (-2)^2 + (-1)^2 + 0^2 + 1^2 + 2^2 = 10
Σ(y – ȳ)^2 = (-20)^2 + (-10)^2 + 0^2 + 10^2 + 20^2 = 1400
- Áp dụng công thức tính độ tuyến tính.
r = (Σ(x – x̄)(y – ȳ)) / (sqrt(Σ(x – x̄)^2) * sqrt(Σ(y – ȳ)^2))
r = 100 / (sqrt(10) * sqrt(1400)) = 0.95
Vậy, độ tuyến tính giữa số giờ học và điểm số của nhóm sinh viên này là 0.95, cho thấy mối quan hệ giữa hai biến là rất mạnh.
Độ tuyến tính và các yếu tố ảnh hưởng
Độ tuyến tính có thể bị ảnh hưởng bởi nhiều yếu tố khác nhau, bao gồm nhiễu và giá trị ngoại la
Tác động của nhiễu và giá trị ngoại lai đến độ tuyến tính
Nhiễu là các giá trị không đúng hoặc bất thường trong tập dữ liệu, khiến cho độ tuyến tính bị giảm đáng kể. Trong trường hợp này, ta cần phải loại bỏ nhiễu khỏi tập dữ liệu để đạt được kết quả chính xác.
Giá trị ngoại lai là các giá trị rất lớn hoặc rất nhỏ so với các giá trị khác trong tập dữ liệu. Khi có giá trị ngoại lai, độ tuyến tính cũng có thể bị ảnh hưởng và sẽ không phản ánh chính xác mối quan hệ giữa hai biến.
Các yếu tố khác ảnh hưởng đến độ tuyến tính
Ngoài nhiễu và giá trị ngoại lai, còn có một số yếu tố khác có thể ảnh hưởng đến độ tuyến tính, bao gồm:
- Sự phi tuyến: mối quan hệ giữa hai biến có thể không phải là tuyến tính, trong trường hợp này, sử dụng độ tuyến tính để đánh giá mối quan hệ sẽ không chính xác.
- Quy mô mẫu: kích cỡ của mẫu dữ liệu có thể ảnh hưởng đến độ tuyến tính. Khi kích cỡ mẫu nhỏ, độ tuyến tính có thể không phản ánh chính xác mối quan hệ giữa hai biến.
- Ràng buộc mẫu: các ràng buộc mẫu khác nhau có thể ảnh hưởng đến độ tuyến tính. Ví dụ, ràng buộc mẫu ngẫu nhiên không giống nhau có thể ảnh hưởng đến độ tuyến tính.
Trong bài viết tiếp theo, chúng ta sẽ tìm hiểu về cách sử dụng độ tuyến tính để đánh giá mối quan hệ giữa hai biến.
Sử dụng độ tuyến tính trong đánh giá mối quan hệ giữa hai biến
Đánh giá mức độ tương quan giữa hai biến
Độ tuyến tính là một công cụ hữu ích để đánh giá mối quan hệ giữa hai biến. Nó cho phép chúng ta xác định mức độ tương quan giữa hai biến và đánh giá liệu mối quan hệ đó có là một mối quan hệ tuyến tính hay không. Nếu mối quan hệ là tuyến tính, thì độ tuyến tính sẽ càng gần với -1 hoặc 1. Nếu mối quan hệ không phải là tuyến tính, thì độ tuyến tính sẽ gần với 0.
Độ tuyến tính cũng cho phép chúng ta đánh giá mức độ tương quan giữa hai biến có phải là một mối quan hệ đồng biến hay nghịch biến không. Nếu độ tuyến tính là âm, thì mối quan hệ là nghịch biến. Nếu độ tuyến tính là dương, thì mối quan hệ là đồng biến.
Dự đoán giá trị của một biến dựa trên giá trị của biến khác
Độ tuyến tính cũng được sử dụng để dự đoán giá trị của một biến dựa trên giá trị của biến khác. Ví dụ, nếu chúng ta muốn dự đoán giá trị của một sản phẩm dựa trên giá trị của một số thuộc tính khác, chúng ta có thể sử dụng độ tuyến tính để xác định mức độ ảnh hưởng của các thuộc tính đó đến giá trị của sản phẩm.
Tuy nhiên, cần lưu ý rằng độ tuyến tính chỉ cho phép chúng ta dự đoán giá trị của một biến dựa trên giá trị của biến khác trong một mối quan hệ tuyến tính. Nếu mối quan hệ giữa hai biến không phải là tuyến tính, thì sử dụng độ tuyến tính để dự đoán giá trị có thể không chính xác.
Ưu điểm và hạn chế của độ tuyến tính
Ưu điểm của độ tuyến tính
Độ tuyến tính có nhiều ưu điểm khi được sử dụng trong thống kê. Đầu tiên, nó là một công cụ đơn giản và dễ sử dụng. Chỉ cần tính toán giá trị độ tuyến tính, chúng ta có thể đánh giá mối quan hệ giữa hai biến.
Thứ hai, độ tuyến tính cho phép chúng ta dự đoán giá trị của một biến dựa trên giá trị của biến khác. Điều này rất hữu ích trong các phân tích hồi quy và dự báo.
Cuối cùng, độ tuyến tính là một công cụ linh hoạt, có thể được sử dụng trong nhiều lĩnh vực khác nhau, từ kinh tế đến khoa học xã hộ
Hạn chế của độ tuyến tính
Tuy nhiên, độ tuyến tính cũng có một số hạn chế. Đầu tiên, nó chỉ đo lường mối quan hệ tuyến tính giữa hai biến. Nếu mối quan hệ giữa hai biến không phải là tuyến tính, thì độ tuyến tính sẽ không phản ánh đầy đủ mối quan hệ đó.
Thứ hai, độ tuyến tính rất nhạy cảm với giá trị ngoại lai và nhiễu. Khi có giá trị ngoại lai hoặc nhiễu, độ tuyến tính có thể bị ảnh hưởng nghiêm trọng, dẫn đến kết quả sai lệch.
Cuối cùng, độ tuyến tính không phản ánh được mối quan hệ nguyên nhân và kết quả giữa hai biến. Nó chỉ đo lường mối quan hệ thống kê giữa hai biến, không giải thích được nguyên nhân của mối quan hệ đó.
Tóm lại, độ tuyến tính là một công cụ hữu ích trong thống kê, nhưng cũng có những hạn chế nên cần được sử dụng cẩn thận và kết hợp với các công cụ khác để đánh giá mối quan hệ giữa hai biến.
FAQ về độ tuyến tính
1. Độ tuyến tính có ảnh hưởng gì đến phân tích thống kê?
Độ tuyến tính là một trong những đại lượng quan trọng trong phân tích thống kê, giúp chúng ta đánh giá mối quan hệ giữa hai biến. Khi phân tích dữ liệu, độ tuyến tính cần được xem xét để đảm bảo độ chính xác của các kết quả phân tích.
2. Làm thế nào để tính toán độ tuyến tính?
Công thức tính toán độ tuyến tính rất đơn giản. Nếu bạn sử dụng phần mềm thống kê, công thức này sẽ được tính tự động. Nếu bạn muốn tính độ tuyến tính thủ công, bạn có thể sử dụng công thức sau:
r = (Σxy – (Σx Σy) / n) / sqrt((Σx^2 – (Σx)^2 / n) (Σy^2 – (Σy)^2 / n))
Trong đó:
- r là độ tuyến tính
- x và y là hai biến
- Σxy là tổng của tích x và y
- Σx và Σy là tổng của x và y
- n là số lượng quan sát
3. Làm thế nào để định nghĩa mối quan hệ giữa hai biến là tuyến tính hoặc phi tuyến tính?
Mối quan hệ giữa hai biến được gọi là tuyến tính nếu nó có thể được biểu diễn bằng một đường thẳng. Ngược lại, mối quan hệ giữa hai biến được gọi là phi tuyến tính nếu nó không thể biểu diễn bằng một đường thẳng. Mối quan hệ phi tuyến tính có thể được biểu diễn bằng các phương trình hàm số khác nhau.
4. Làm thế nào để đánh giá mức độ tương quan giữa hai biến?
Độ tuyến tính được sử dụng để đánh giá mức độ tương quan giữa hai biến. Giá trị của độ tuyến tính nằm trong khoảng từ -1 đến 1. Nếu giá trị của độ tuyến tính tiến gần đến -1 hoặc 1, thì mối quan hệ giữa hai biến càng mạnh. Nếu giá trị độ tuyến tính bằng 0, thì hai biến không có mối quan hệ tuyến tính nào cả.
5. Độ tuyến tính có hạn chế gì?
Độ tuyến tính có một số hạn chế, đặc biệt là khi mối quan hệ giữa hai biến không phải là tuyến tính. Độ tuyến tính cũng không thể xác định mối quan hệ nhân quả giữa hai biến.
